What is Free Space Path Loss?
Imaginary space where no matter exists is called free space. Free Space Path Loss (FSPL) is loss when electromagnetic wave pass through free space.
When calculating link budget, there are losses because of atmosphere, rain, polarization, etc. FSPL is the biggest loss in various loss.
Dervation of Free Space Path Loss
From Friss transmission equation, relation between the transmission power from transmission antenna and power received at receiving antenna is described as:
\[\frac{P_r}{P_t} = \left(\frac{\lambda}{4\pi d}\right)^2G_tG_r\]
where \(\lambda\) is wave length, \(d\) is distance between antenas, \(G_t\) is gain of transmission antenna,\(G_r\) is gain of receiving antenna.
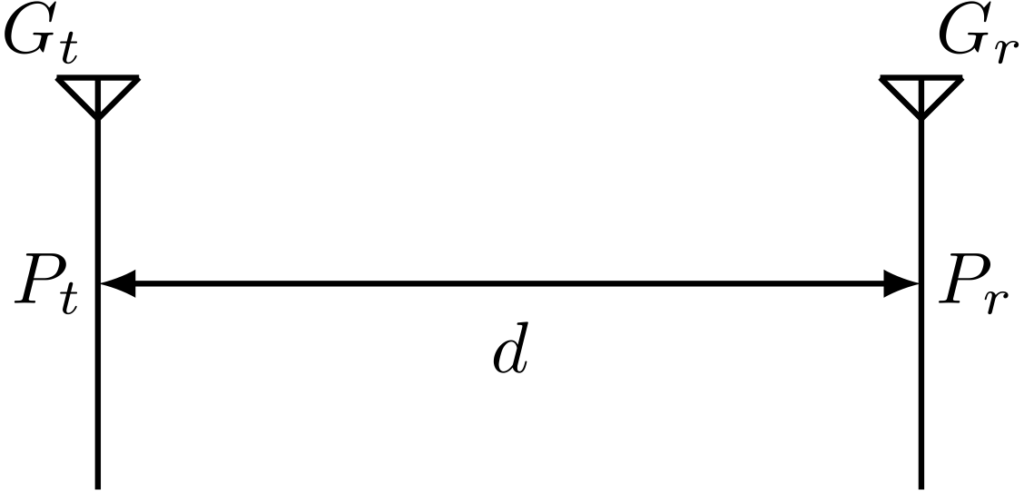
Here, supposing \(G_t=1\), \(G_r=1\) (gain of antennas are zero),
\[\frac{P_r}{P_t} = \left(\frac{\lambda}{4\pi d}\right)^2 = \frac{\displaystyle 1}{\displaystyle \left(\frac{4\pi d}{\lambda}\right)^2}\]
thus, free space path loss \(L_{fsp}\) is
\[L_{fsp} = \left(\frac{4\pi d}{\lambda}\right)^2\]
calculation of free space path loss
Link budget uses dB, thus convert unit into dB.
From \(c\) is speed of light, \(f\) is frequency of carrier wave and \(\lambda = \frac{\displaystyle c}{\displaystyle f}\),
\[\begin{align}
L_{fsp} = 10\log{\left(\frac{4\pi d}{\lambda}\right)^2} &= 20\log{\frac{4\pi d}{\lambda}} \\
&= 20\log{\frac{4\pi df}{c}} \\
&= 20\log{\frac{4\pi}{c}}+20\log{d}+20\log{f} \\
&= 92.45+20\log{d}+20\log{f} \\
\end{align}\]
where the unit of \(d\) is \(\mathrm{km}\), \(f\) is \(\mathrm{GHz}\).
other unit combination calculating \(L_{fsp}\) is as follows.
When \(d[\mathrm{m}]\),\(f[\mathrm{kHz}]\),
\[L_{fsp} = -87.55+20\log{d}+20\log{f}\]
When \(d[\mathrm{m}]\),\(f[\mathrm{MHz}]\),
\[L_{fsp} = -27.55+20\log{d}+20\log{f}\]
When \(d[\mathrm{km}]\),\(f[\mathrm{MHz}]\),
\[L_{fsp} = 32.44+20\log{d}+20\log{f}\]