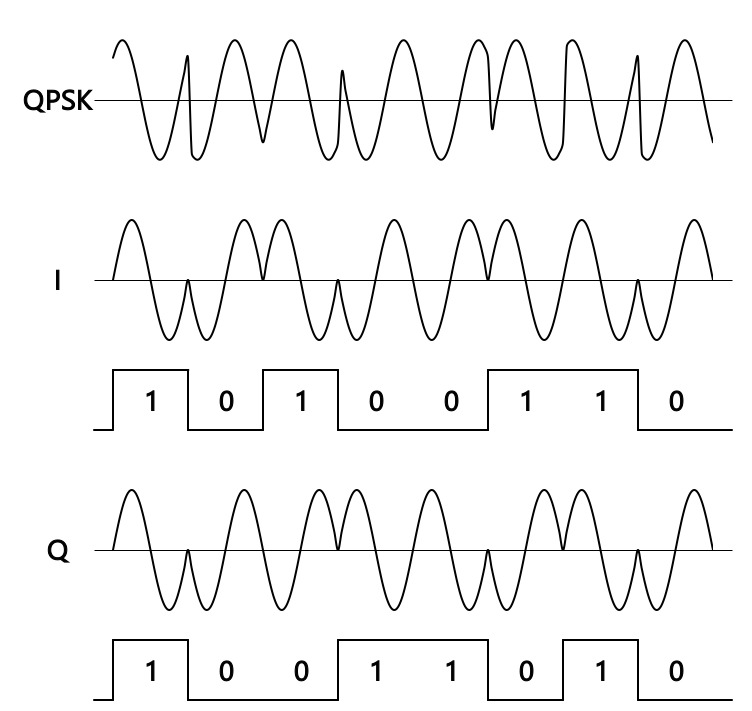
QPSK is the abbreviation of Quadrature Phase-Shift Keying, which is the phase modulation method using four phases.
The signal of QPSK can be represented as:
\[s(t) = A\cos{(2\pi ft+\phi)}\]
where \(A\) is the amplitude of carrier wave, \(f\) is the frequency of carrier wave and \(\phi\) is the phase which changes depending on the signals:
- when 11, \(\phi = \pi/4\)
- when 01, \(\phi = 3\pi/4\)
- when 00, \(\phi = -3\pi/4\)
- when 10, \(\phi = -\pi/4\)
Furthermore, expanding \(s(t)\),
\[\begin{eqnarray}s(t) & = & A\cos{(2\pi ft+\phi)} \& = & A\cos{(2\pi ft)}\cos{(\phi)} – A\sin{(2\pi ft)}\sin{(\phi)} \& = & \frac{I}{\sqrt{2}}A\cos{(2\pi ft)} – \frac{Q}{\sqrt{2}}A\sin{(2\pi ft)} \end{eqnarray}\]
where \(I = \sqrt{2}\cos{\phi}\) and \(Q = \sqrt{2}\sin{\phi}\) also stasifies the following conditions:
- when 11, \(I = 1, Q = 1\)
- when 01, \(I = -1, Q = 1\)
- when 00, \(I = -1, Q = -1\)
- when 10, \(I = 1, Q = -1\)
Thus, QPSK can be regarded as the superposition of BPSK whose phase shifted for 90 degrees.
In this case, each BPSK signal are called I-channel and Q-channel.
QPSK signal can be plotted as: