View factor is used in calculation of energy transfered by radiation.
This article explains the definition and derivation of view factor.
Definition of View Factor
Suppose there are plane \(i\) and plane \(j\) in vacuum space.
The area of plane \(i\) and plane \(j\) are \(A_i\) and \(A_j\).
Here, the energy tranfered from plane \(i\) can be written as:
この時、面\(i\)から放射されるエネルギーは、放射強度を\(i_i\)(単位立体角あたりの放射エネルギー)とすると、
\[Q_i = \pi i_iA_{i}\]
where \(i_i\) is the radiation strength (radiation energy per unit solid angle).
Of total energy radiated from plane \(i\), the ratio of energy transfered to plane \(j\), \(F_{ij}\) should be:
\[F_{ij} = \frac{Q_{ij}}{Q_{i}} = \frac{Q_{ij}}{\pi i_iA_{i}}\]
This \(F_{ij}\) is called view factor.
Derivation of View Factor
Suppose there are infinitesimal areas \(dA_i\) and \(dA_j\) on plane \(i\) and plane \(j\), and define the distance between them as \(r\).
Also, define the angle between normal vector of planes and the distance \(r\) ad \(\phi_i\) and \(\phi_j\) as shown below.
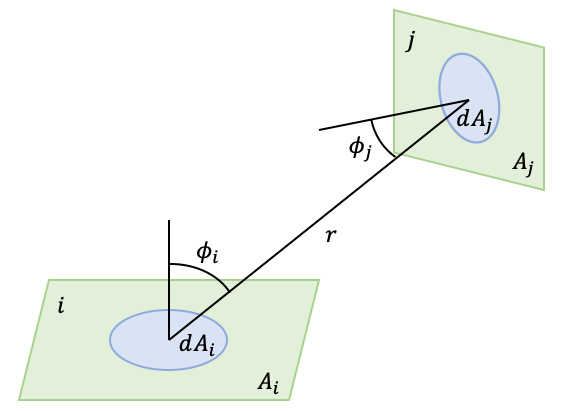
Suppose that \(dQ_{ij}\) denotes the energy from \(dA_i\) to \(dA_j\),
\[dQ_{ij} = i_{i}dA_{i}\cos{\phi_{i}}d\omega\]
where \(d\omega\) is solid angle,
\[d\omega = \frac{dA_{j}\cos{\phi_{j}}}{r^2}\]
Thus, \(dQ_{ij}\) can be written as:
\[dQ_{ij} = i_{i}\frac{\cos{\phi_{i}}\cos{\phi_{j}}}{S^2}dA_{i}dA_{j}\]
Integrating this equation, the following equation can be obtained:
\[F_{ij} = \frac{Q_{ij}}{Q_{i}} = \frac{1}{\pi A_{i}}\int_{A_{i}}\int_{A_{j}}\frac{\cos{\phi_{i}}\cos{\phi_{j}}}{r^2}dA_{i}dA_{j}\]