自由空間伝搬損失とは
物質が存在しない仮想的な空間を自由空間と呼びます.自由空間伝搬損失(Free Space Path Loss)とは電磁波が自由空間を通る時に受ける減衰のことです.FSPLと描かれることがあります.
回線計算を行う際には,自由空間伝搬損失だけでなく,大気や降雨,偏波の影響などを考慮する必要がありますが,自由空間伝搬損失は各種損失の中でも一番大きな損失となります.
ここではその計算式をフリスの公式から導出していきます.
自由空間伝搬損失の導出
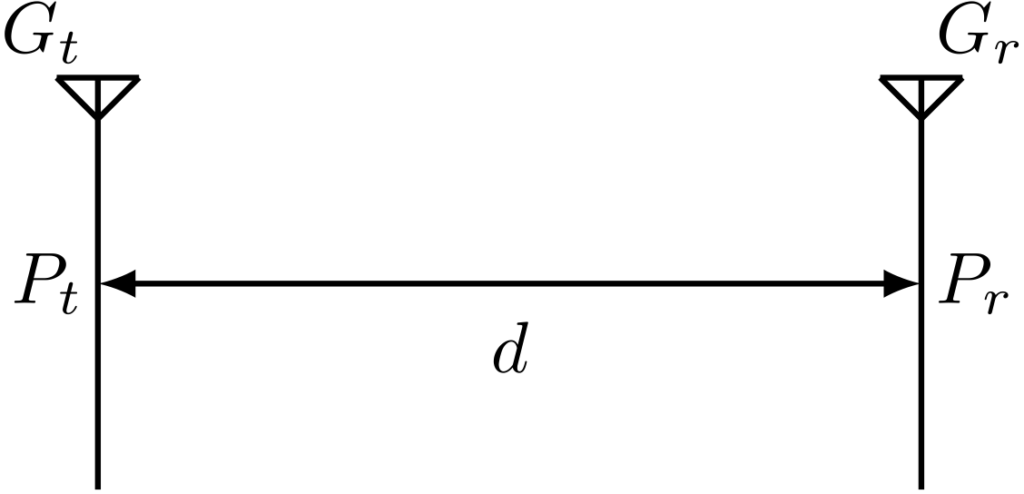
フリスの伝達公式より,送信アンテナから送信される電力\(P_t\)と,受信アンテナで受信する電力\(P_r\)の関係は次の式で表されます.
\[\frac{P_r}{P_t} = \left(\frac{\lambda}{4\pi d}\right)^2G_tG_r\]
ただし,\(\lambda\)は波長,\(d\)はアンテナ間の距離,\(G_t\)は送信アンテナの利得,\(G_r\)は受信アンテナの利得です.
ここで,\(G_t=1\),\(G_r=1\)(送信アンテナ,受信アンテナともにゲインが0)と仮定すると,
\[\frac{P_r}{P_t} = \left(\frac{\lambda}{4\pi d}\right)^2 = \frac{\displaystyle 1}{\displaystyle \left(\frac{4\pi d}{\lambda}\right)^2}\]
よって,自由空間伝達損失\(L_{fsp}\)は,
\[L_{fsp} = \left(\frac{4\pi d}{\lambda}\right)^2\]
となります.以上で自由空間伝搬損失の導出ができました.
自由空間伝搬損失の計算式
回線計算などではdBで計算するため,単位をdBに変換します.
\(c\)を光速,\(f\)を搬送波周波数とすると,\(\lambda = \frac{\displaystyle c}{\displaystyle f}\)より,
\[\begin{align}
L_{fsp} = 10\log{\left(\frac{4\pi d}{\lambda}\right)^2} &= 20\log{\frac{4\pi d}{\lambda}} \\
&= 20\log{\frac{4\pi df}{c}} \\
&= 20\log{\frac{4\pi}{c}}+20\log{d}+20\log{f} \\
&= 92.45+20\log{d}+20\log{f} \\
\end{align}\]
と表せます.ただし,\(d\)の単位は\(\mathrm{km}\),\(f\)の単位は\(\mathrm{GHz}\)です.
他の単位の組み合わせでの\(L_{fsp}\)は次のようになります.
\(d[\mathrm{m}]\),\(f[\mathrm{kHz}]\)のとき
\[L_{fsp} = -87.55+20\log{d}+20\log{f}\]
\(d[\mathrm{m}]\),\(f[\mathrm{MHz}]\)のとき
\[L_{fsp} = -27.55+20\log{d}+20\log{f}\]
\(d[\mathrm{km}]\),\(f[\mathrm{MHz}]\)のとき
\[L_{fsp} = 32.44+20\log{d}+20\log{f}\]