雑音指数の定義
受信システムにおけるアンプの性能を表すものとして、雑音指数(Noise Figure, NF)がある。
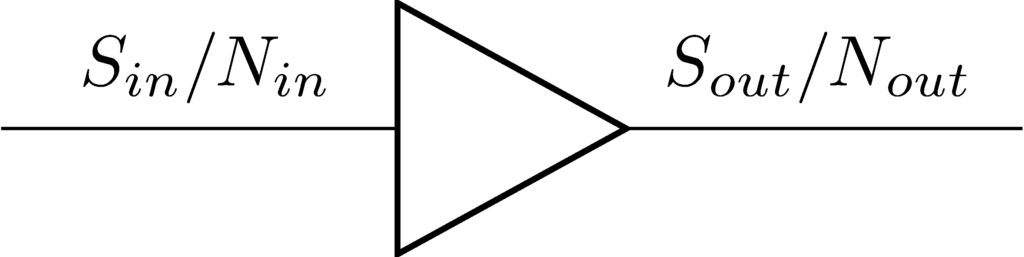
雑音指数の真数\(f\)は入力S/Nと出力S/Nの比で、次のように表される。
\[f = \frac{S_{in}/N_{in}}{S_{out}/N_{out}}\]
dB表記の場合は
\[NF = 10\log{f}\]
となる。
等価入力雑音温度
アンプのゲインを\(G\)とすると、
\[S_{out} = GS_{in}\]
と書ける。また、周辺温度を\(T_{0}\)とすれば、
\[N_{in} = kT_{0}B\]
となる。ただし、\(k\)はボルツマン定数、\(B\)は帯域幅である。
また、アンプの等価入力雑音温度を\(T_{G}\)とすると、
\[N_{out} = G(kT_{0}B+kT_{G}B)\]
となる。以上より、
\[f = \frac{S_{in}/kT_{0}B}{GS_{in}/G(kT_{0}B+kT_{G}B)}\]
\[f = 1+\frac{T_{G}}{T_{0}}\]
と表すことができる。
この式から、雑音指数は必ず1以上になることがわかる。また、
\[T_{G} = (f-1)T_{0}\]
と書けば、アンプの等価入力雑音温度が分かる。
フリスの公式
ゲインがそれぞれ\(G_1\)、\(G_2\)であるアンプが2段ある状況を考える。

雑音指数の定義から
\[\frac{N_{o1} + G_1N_{in}}{G_1N_{in}} = F_1\]
\[\frac{N_{o2} + G_2N_{in}}{G_2N_{in}} = F_2\]
各アンプでの雑音は
\[N_{o1} = (F_1-1)G_1N_{in}\]
\[N_{o2} = (F_2-1)G_2N_{in}\]
最終段が出力する雑音は
\[\begin{eqnarray}
N_2 & = & N_{o2} + G_2N_1 \\
& = & N_{o2} + G_2(N_{o1} + G_1N_{in}) \\
& = & N_{o2} + G_2N_{o1} + G_2G_1N_{in} \\
& = & (F_2-1)G_2N_{in} + F1G_1G_2N_{in}
\end{eqnarray}\]
よって、系全体の雑音指数(真数)は
\[F_{total} = \frac{S_{in}/N_{in}}{S_{out}/N_{out}} = \frac{S_{in}/N_{in}}{G_1G_2S_{in}/N_2} = \frac{N_2}{G_1G_2N_{in}}\]
\[F_{total} = F_1 + \frac{F_2-1}{G_1}\]
となる。これをN段のアンプに拡張すれば、
\[F_{total} = F_1 + \frac{F_2-1}{G_1} + \frac{F_3-1}{G_1G_2} + \cdots \]
となる。これはフリスの雑音公式と呼ばれる。この公式から、\(F_2\)以降の雑音指数は前段までのゲインで除算されるため、系全体の雑音指数は初段のアンプの雑音指数が支配的だと言える。受信機の初段のアンプの性能が受信機の性能を決定するため、アンテナの直後にLNAを配置することが多い。