衛星通信で誤り訂正のためによく使われる符号として、畳み込み符号がある。
畳み込み符号は前方誤り訂正(Forward Error Correction, FEC)の1種である。
畳み込み符号化
畳み込み符号は、衛星通信でよく使われる誤り訂正符号の1つである。
畳み込み符号化は、データの中に「枠」を作り、枠の中のデータから一定の規則に沿って新しいデータを作り出す操作のことをいう。
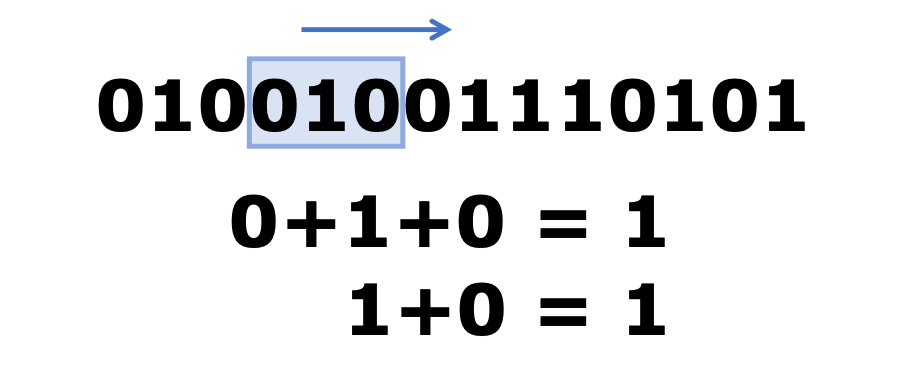
枠は右に1ビットずつスライドしていく。
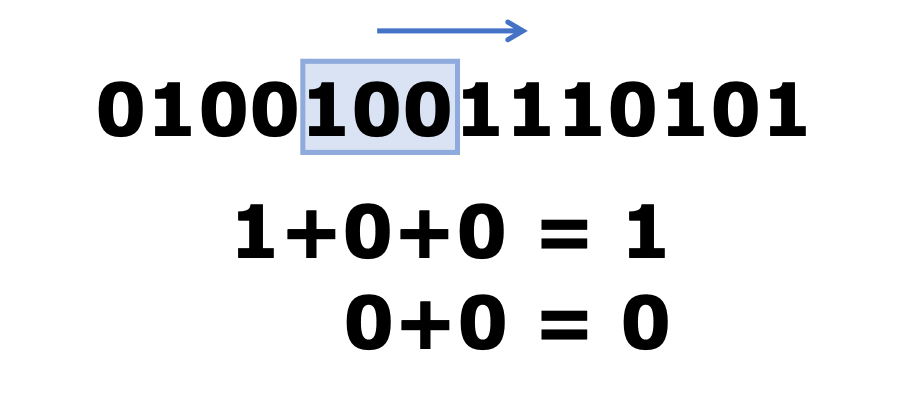
枠の大きさのことを拘束長と呼び、上の場合は拘束長\(K=3\)となる。
枠を1ビットずつスライドさせるとき、新しく作られたデータ(パリティビット)のビット数を\(r\)とすると、\(1/r\)のことを符号化率と呼び、上の場合は符号化率\(R=1/2\)となる。
NASAのボイジャー計画で符号化率\(R=1/2\)、拘束長\(K=7\)の畳み込み符号が採用されて以来、この組み合わせが広く使われている。
拘束長が長ければビットエラーに対して強くなるが、デコードに必要な計算量が増えるため、ビット誤り率の要求とコンピュータの性能を考慮して設計する必要がある。
上の図の例を数式で表す。データ列を\(x\)、パリティビット列を\(p\)とすると、
\[\begin{align}
p_n^0 &= x_n+x_{n-1}+x_{n-2} \\
p_n^1 &= x_n+x_{n-1}
\end{align}\]
この式は、次のように書くこともできる。
\[\begin{align}
p_n^0 &= 1\cdot x_n+1\cdot x_{n-1}+1\cdot x_{n-2} \\
p_n^1 &= 1\cdot x_n+1\cdot x_{n-1}+0\cdot x_{n-2}
\end{align}\]
となる。このようにデータとパリティビットを関係づける多項式のことを生成多項式と呼ぶ。
生成多項式の係数を、上から\(g^0=(1,1,1)\)、\(g^1=(1,1,0)\)とすれば、パリティビットは、
\[p^i_n = (\sum_{j=0}^{k-1} g_j^i x_{n-j}) \bmod 2\]
と表すことができる。これは、\(g\)と\(x\)の畳み込み積分をインパルス応答に沿って行なったものである。
これが畳み込み符号化と呼ばれる理由である。
具体例
次のデータ列に対して畳み込み符号化を行う。
\[[1,0,1,1]\]
ただし、符号化率\(R=1/2\)、拘束長\(K=3\)とし、生成多項式\(g\)は
\[\begin{align}
g^0=(1,1,1) \\
g^1=(1,1,0)
\end{align}\]
とする。
\[\begin{align}
p_0^0 &= 1+0+0 = 1\\
p_0^1 &= 1+0 = 1\\
p_1^0 &= 0+1+0 = 1\\
p_1^1 &= 0+1 = 1\\
p_2^0 &= 1+0+1 = 0\\
p_2^1 &= 1+0 = 1\\
p_3^0 &= 1+1+0 = 0\\
p_3^1 &= 1+1 = 0
\end{align}\]
よって、データ列\([1,0,1,1]\)は、畳み込み符号化によって\([1,1,1,1,0,1,0,0]\)と変換される。