全地球測位システム(Global Positioning System, GPS)は、衛星を用いて位置と時刻を測定するためのシステムで、アメリカ合衆国宇宙軍(United States Space Force)によって所有・運用されている。
動作原理
衛星は測距信号を送信する機能を持つ。
この信号を4機の衛星から同時に受信し、その受信データから衛星と受信機の幾何関係から導かれる連立方程式を立てる。
この連立方程式を解くことで受信機の位置と時刻を決定する。
測距信号
測距信号はC/A (Coarse/Acquisition) コードと航法メッセージがある。
C/Aコードは擬似距離を計算するための擬似ランダム信号(Psuedo Random Noise, PRN)で、1023ビットを1msで送信する。
航法メッセージは次の情報を含む。
- 送信時の衛星時刻
- 衛星位置
- 衛星Health
- 衛星時刻修正
送信されたC/Aコードと受信機側で生成したPRNコードの相関をとることで衛星を特定する。
C/Aコード
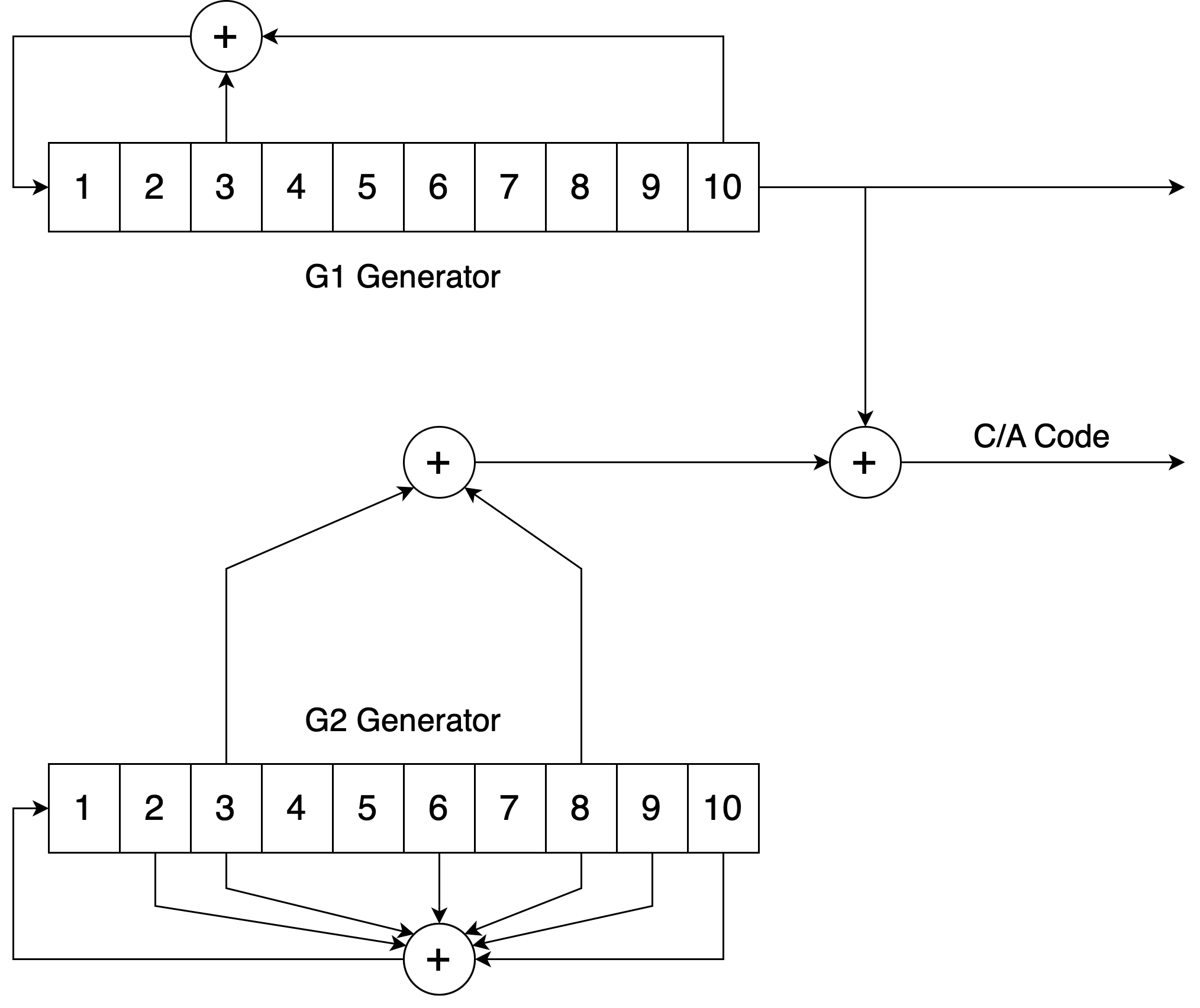
連立方程式
衛星の座標を\((x_i,y_i,z_i)\)、受信機の座標を\(x,y,z\)とする。
衛星が電波を送信した時の衛星の時刻を\(t_{tx,i}\)、受信機が電波を受信した時の受信機の時刻を \(t_{rx}\) とする。
衛星が電波に時刻情報を載せて送信することで、受信機側では\(t_{rx}-t_{tx,i}\)によって電波が衛星から受信機に届くまでにかかった時間\(t\)が計算できる。
しかし、実際には衛星と受信機の時計にはズレがあるため、受信機の時計の衛星の時計からのずれを\(d\)とすると、
\[(x-x_1)^2+(y-y_1)^2+(z-z_1)^2 = (c(t-d))^2\]
とすることができる。
この式の未知数は4つ\(x,y,z,d\)であるため、4つの衛星に対して
\[\begin{eqnarray}
(x-x_1)^2+(y-y_1)^2+(z-z_1)^2 & = (c(t-d_1))^2 \\
(x-x_2)^2+(y-y_2)^2+(z-z_2)^2 & = (c(t-d_2))^2 \\
(x-x_3)^2+(y-y_3)^2+(z-z_3)^2 & = (c(t-d_3))^2 \\
(x-x_4)^2+(y-y_4)^2+(z-z_4)^2 & = (c(t-d_4))^2 \\
\end{eqnarray}\]
と式を立てて、これを解くことで受信機の座標を計算することができる。
ただし、衛星はすべて時刻を一致しているとする。(衛星には原子時計が搭載されており、正確な時刻を持っていると考えることができる)
また、拡散方式によって、受信機側はアンテナが一つでも衛星を区別できる。
受信した衛星の位置・時刻データから、受信機の位置を求める。具体的には、衛星と受信機の位置関係から求められる連立方程式を解く。