π型アッテネータは、1つの直列抵抗器と、2つのシャント抵抗器からなる信号減衰器である。抵抗値とインピーダンスから減衰量を、または減衰量とインピーダンスから抵抗値を求めることができる。
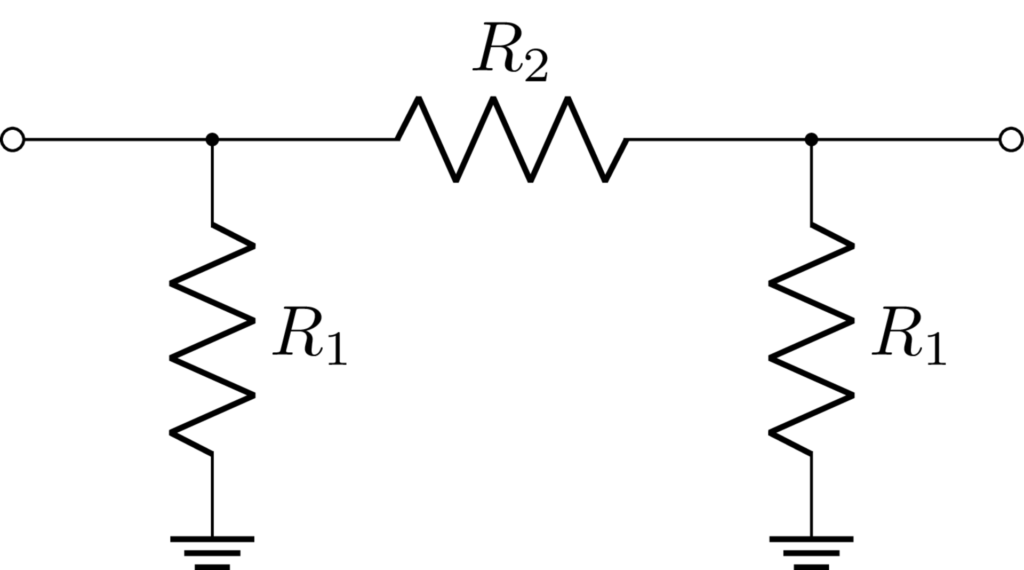
減衰量とインピーダンスから抵抗値の計算
dB
Ω
抵抗値とインピーダンスから減衰量の計算
計算式
減衰量\(K_{\mathrm{dB}}\)は以下のように定義される。
\[K_{\mathrm{dB}} = 10\log_{10}\left(\frac{P_{\mathrm{in}}}{P_{\mathrm{out}}}\right) = 20\log_{10}\left(\frac{V_{\mathrm{in}}}{V_{\mathrm{out}}}\right)\]
ここで、
\[K = \frac{V_{\mathrm{in}}}{V_{\mathrm{out}}} = 10^{\frac{K_{\mathrm{dB}}}{20}}\]
と置く。
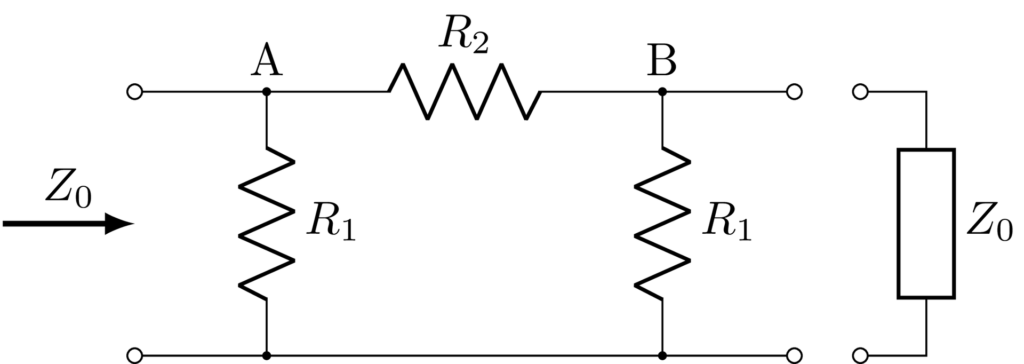
減衰量から抵抗値の計算
点Aにおいて、キルヒホッフの第1法則より、
\[\frac{V_{\mathrm{in}}}{Z_0} = \frac{V_{\mathrm{in}}}{R_1} + \frac{V_{\mathrm{in}}-V_{\mathrm{out}}}{R_2} \tag{1}\]
同様に、点Bにおいて、
\[\frac{V_{\mathrm{in}}-V_{\mathrm{out}}}{R_2} = \frac{V_{\mathrm{out}}}{Z_0}+\frac{V_{\mathrm{out}}}{R_1} \tag{2}\]
(1)+(2)より、
\[\frac{V_{\mathrm{in}}}{Z_0}-\frac{V_{\mathrm{in}}}{R_1} = \frac{V_{\mathrm{out}}}{R_1}+\frac{V_{\mathrm{out}}}{Z_0}\]
\[\frac{K}{Z_0}-\frac{K}{R_1} = \frac{1}{Z_0}+\frac{1}{R_1}\]
\[K\cdot\frac{R_1-Z_0}{R_1Z_0} = \frac{R_1+Z_0}{R_1Z_0}\]
\[K(R_1-Z_0) = R_1+Z_0\]
\[(K-1)R_1 = (K+1)Z_0\]
\[R_1 = \frac{K+1}{K-1}Z_0 \tag{3}\]
(2),(3)式より、
\[
\begin{aligned}
\frac{K-1}{R_2} &= \frac{1}{Z_0} + \frac{1}{R_1} \\
&= \frac{1}{Z_0} + \frac{K-1}{(K+1)Z_0} \\
&= \frac{2K}{(K+1)Z_0}
\end{aligned}
\]
よって、
\[R_2 = \frac{K^2-1}{2K}Z_0\]
抵抗値から減衰量の計算
分圧の法則より、
\[
\begin{aligned}
K &= \frac{V_{\mathrm{in}}}{V_{\mathrm{out}}} \\
&= \frac{R_2 + (R_1 \parallel Z_0)}{R_1 \parallel Z_0} \\
&= \frac{R_2+\frac{R_1Z_0}{R_1+Z_0}}{\frac{R_1Z_0}{R_1+Z_0}} \\
&= \frac{R_2(R_1+Z_0)}{R_1Z_0} + 1
\end{aligned}
\]
キーワード
- 影像インピーダンス