放射伝熱において、伝達するエネルギー量を計算するために必要な形態係数について説明します。
この記事では形態係数の定義とその計算式の導出について取り扱います。
形態係数の定義
まず、真空の空間に面\(i\)と面\(j\)があるとします。
面\(i\)と面\(j\)の面積をそれぞれ\(A_i\)、\(A_j\)とします。
この時、面\(i\)から放射されるエネルギーは、放射強度を\(i_i\)(単位立体角あたりの放射エネルギー)とすると、
\[Q_i = \pi i_iA_{i}\]
と表されます。ここで、面\(i\)から放射される全エネルギーのうち、面\(j\)に入るエネルギーの割合\(F_{ij}\)は、
\[F_{ij} = \frac{Q_{ij}}{Q_{i}} = \frac{Q_{ij}}{\pi i_iA_{i}}\]
となります。この\(F_{ij}\)を形態係数と呼びます。
形態係数の計算式の導出
面\(i\)、\(j\)上に微小面積\(dA_i\)、\(dA_j\)を考え、それらの距離を\(r\)とします。
また、この距離\(r\)が微小面積の法線となす角をそれぞれ\(\phi_i\)、\(\phi_j\)とします。
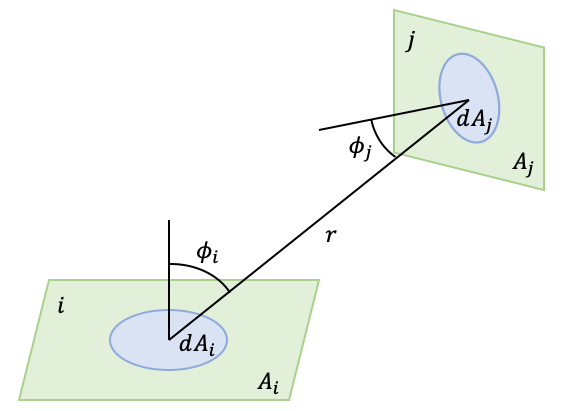
\(dA_i\)から出て\(dA_j\)に入る熱量を\(dQ_{ij}\)とすると、
\[dQ_{ij} = i_{i}dA_{i}\cos{\phi_{i}}d\omega\]
となります。ただし、\(d\omega\)は立体角で、
\[d\omega = \frac{dA_{j}\cos{\phi_{j}}}{r^2}\]
です。以上より、
\[dQ_{ij} = i_{i}\frac{\cos{\phi_{i}}\cos{\phi_{j}}}{S^2}dA_{i}dA_{j}\]
となり、これをそれぞれの面で積分して、
\[F_{ij} = \frac{Q_{ij}}{Q_{i}} = \frac{1}{\pi A_{i}}\int_{A_{i}}\int_{A_{j}}\frac{\cos{\phi_{i}}\cos{\phi_{j}}}{r^2}dA_{i}dA_{j}\]
となります。これが形態係数の計算式になります。