回線設計とは
衛星と地上局,または衛星同士の通信を実現するため,通信仕様を決定する作業のことを回線設計(Link Design)と呼びます.
回線設計では,仕様決定,回線計算,評価のステップを繰り返し行い,最終的な通信仕様を決定します.
ここでは回線計算について詳しく説明します.
回線計算の方法
回線計算は最終的に,回線マージンを算出します.
回線マージンは,通信仕様から計算した受信\(C/N_0\)と受信に必要となる要求\(C/N_0\)の差で表されます.
この回線マージンの大きさを考慮して仕様を決定していきます.
EIRP
EIRPは、equivalent isotropically radiated power(等価等方放射電力),またはeffective isotropically radiated power (実効等方放射電力) の略で,電波の強さを表します.
\(P_t[\mathrm{dBW}]\)を送信電力,\(L_{ft}[\mathrm{dB}]\)を送信機-送信アンテナ間の給電線損失,\(G_t[\mathrm{dBi}]\)を送信アンテナの利得とすると,
\[\mathrm{EIRP} = P_t-L_{ft}+G_t\]
と与えられます.
自由空間伝搬損失(free space path loss)
自由空間伝搬損失は,物質が存在しない仮想的な空間(自由空間)を伝搬する電磁波が受ける減衰のことを指します.
\(d[\mathrm{km}]\)をアンテナ間の距離,\(\lambda[\mathrm{km}]\)を波長,\(f[\mathrm{GHz}]\)を送信アンテナ利得とすると,自由空間伝搬損失\(L_{fsp}\)は,
\[L_{fsp} = 10\log{\left(\frac{4\pi d}{\lambda}\right)^2} = 92.45+20\log{d}+20\log{f} \]
と表されます.
受信G/T
受信\(\mathrm{G/T}\)は受信利得とシステム雑音温度の比で,受信設備の性能を表します.
\(G_r[\mathrm{dBi}]\)を受信アンテナの利得,\(L_{fr}[\mathrm{dB}]\)を受信アンテナ-受信機間の給電線損失,\(T_s[\mathrm{dBK}]\)をシステム雑音温度とすると,
\[\mathrm{G/T} = G_r-L_{fr}+T_s\]
となります.また,
\[T_s = 10\log{(T_{ant}/L+T_f(1-1/L)+T_e)}\]
です.ただし,\(T_{ant}[\mathrm{K}]\)はアンテナ雑音温度,\(T_f[\mathrm{K}]\)は給電線雑音温度,\(T_e[\mathrm{dBK}]\)は受信機雑音温度です.
受信機雑音温度\(T_e\)は,雑音指数\(\mathrm{NF}\)を用いて,
\[T_e = (\mathrm{NF}-1)T_0\]
とも書けます.ただし,\(T_0=290K\)です.
受信C/N0
\(\mathrm{C/N_0}\)は搬送波対雑音密度比(Carrier to Noise densirty ratio)と呼ばれ,搬送波電力と雑音電力密度の比を表します.
受信\(C/N_0\)は,各種損失を無視すれば,次のようになります.
\[\mathrm{C/N_0} = \mathrm{EIRP}-L_{fsp}+G/T+228.6\]
要求Eb/N0
\(\mathrm{E_b/N_0}\)は1ビット当たりのエネルギーと雑音電力密度の比を表します.
要求されるビット誤り率(BER:Bit Error Rate)を基準に要求\(\mathrm{E_b/N_0}\)を決定します.
決定には下の図を使います.
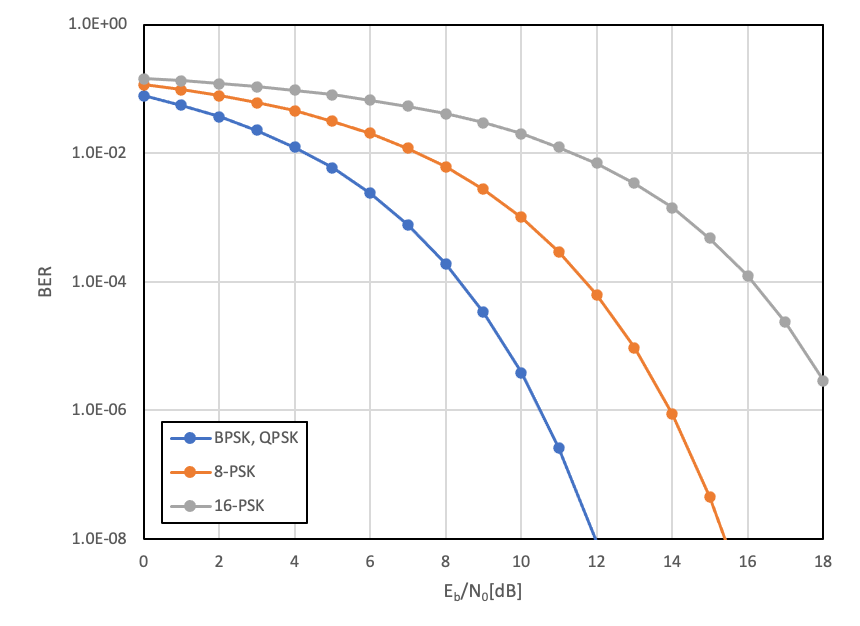
変調方式によっても必要な\(\mathrm{E_b/N_0}\)は違います.
代表的な\(\mathrm{E_b/N_0}\)の値を示しておきます.
| BER | BPSK,QPSK | 8-PSK | 16-PSK |
| 10-5 | 9.6dB | 13dB | 17.6dB |
符号化利得
データ伝送において,誤り訂正符号などの符号を用いることで有利になることがあります.
代表的な符号化方式とその符号化利得を次に示します.
| 軟判定ビタビ復号 | 3dB |
| 硬判定ビタビ復号 | 5.2dB |
変調損失
信号を変調する際に生じる損失を変調損失と呼びます.
これは3dB程度です.
要求C/N0
通信に必要な\(\mathrm{C/N_0}\)を要求\(\mathrm{C/N_0}\)と呼びます.
\(\mathrm{(E_b/N_0)_req}\)を要求\(\mathrm{E_b/N_0}\),\(G_c\)を符号化利得,\(L_m\)を変調損失,\(R\)をデータレートとすると,
\[\mathrm{C/N_0} = \mathrm{(E_b/N_0)_req}-G_c+L_m+R\]
となります.
回線マージン
受信\(\mathrm{C/N_0}\)から要求\(\mathrm{C/N_0}\)を引いた値となります.